Computational Electromagnetics
Published:
A High–Order Perturbation of Surfaces/Asymptotic Waveform Evaluation (HOPS/AWE) algorithm for Grating Scattering Problems.
Published:
A High–Order Perturbation of Surfaces/Asymptotic Waveform Evaluation (HOPS/AWE) algorithm for Grating Scattering Problems.

Published:
Computer implementation of the Riemann Siegel formula in Julia alongside various plotting and numerical programs related to the Riemann zeta function.
Published:
A collection of ML projects including linear/logistic regression, time series analysis, natural language processing, unsupervised ML, self-supervised ML, and LLMs.
Published:
An alternative technique to FDM/FEM/SEM for solving partial differential equations numerically.

Published:
A recommender system for travel destinations through the popular website Trip Advisor.
Published in University of Michigan Deep Blue System, 2015
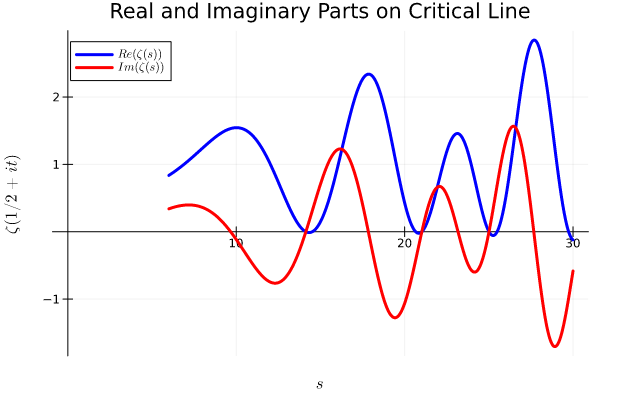
This project focuses on exploring different computational methods of the Riemann Zeta function. The zeta function is formally defined as $\zeta(s)$ and the Riemann Hypothesis states that all non-trivial zeros of $\zeta(s)$ lie on the critical line where $\Re(s) = 1/2$. Modern research and advanced algorithms have not been able to disprove the Riemann Hypothesis. More recently, a variation of the Odlyzko-–Schönhage algorithm has verified the Riemann Hypothesis up to $10^{13}$ zeros. This project is composed of two major programs which calculate functional values and zeros of the Riemann zeta function. The first program calculates $\zeta(s)$ for any value of $s$ provided $s\in\mathbb{R}$ through what is known as the Cauchy-Schlömilch transformation. The second program uses the well known Riemann–Siegel formula. Prior to the work done inside the Odlyzko–Schönhage algorithm, this was the method of choice for finding zeros of $\zeta(s)$. The algorithm is heavily dependent on locating sign changes of the Riemann-Siegel $Z$ function in order to find zeros on the critical line. Loosely speaking, one can derive this formula from a direct relationship that was originally found by Siegel which states that $Z(t) = e^{i \theta(t)} \zeta\left(\frac{1}{2}+it\right)$.
Download here
Published in UIC Electronic Thesis and Dissertation (ETD) System, 2022
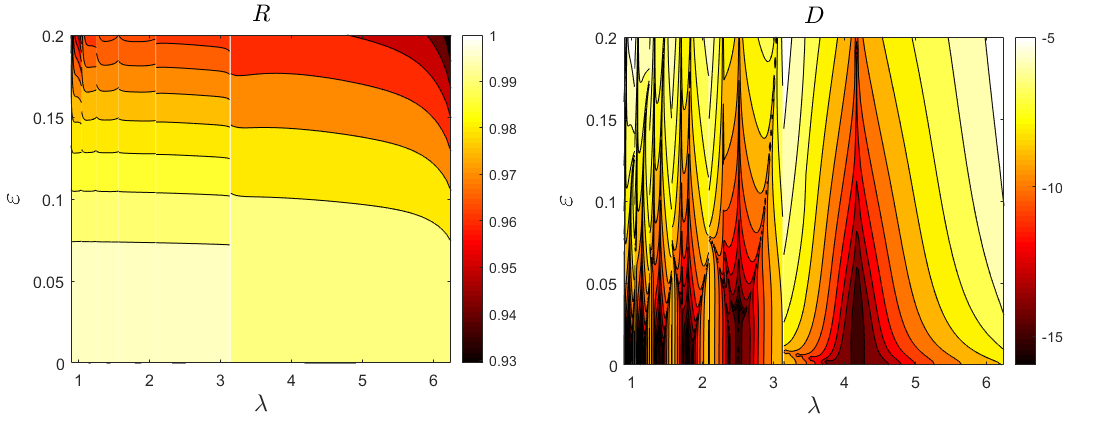
This thesis presents rigorous analytical and numerical results necessary for the numerical analysis of a class of High–Order Perturbation of Surfaces/Asymptotic Waveform Evaluation (HOPS/AWE) methods in a laterally periodic two–layer structure. Numerical simulations of scattering returns from periodic diffraction gratings are crucial to a large number of applications in physics and engineering, and the work presented here examines methods for numerically modeling scattering returns from such structures. The strategies presented in this thesis represent the results of our efforts towards the dual goals of 1) Proving a theorem on the existence and uniqueness of solutions to a system of partial differential equations which model the interaction of linear waves in periodic layered media and 2) Developing a numerical algorithm to record scattered energy through a novel interfacial method that is perturbative in nature. The first of our goals is established through classical methods based on the theory of Sobolev spaces and regular perturbation theory. The proof involves several rigorous analyses, and we formulate the scattering problem in terms of Dirichlet–Neumann Operators which are computed using the Transform Field Expansion methodology. A novelty of our approach is the joint analyticity of solutions with respect to both geometry and frequency perturbations. The theory itself is then validated through our second goal which is the development of a joint HOPS/AWE algorithm. For this, we develop a special class of interfacial numerical algorithms that are well–suited to periodic diffraction problems. Our algorithm calculates the Reflectivity Map, $R$, which measures the response (reflected energy) of a periodically corrugated grating structure as a function of its illumination frequency. Moreover, we present a series of challenging and physically relevant numerical experiments to validate the scattering results expected by our algorithm. Forthcoming research will focus on extending the proof of analyticity to additional parameters relevant to the geometry of the structure, increasing the complexity of the structure through generalizing our results to any finite number of layered interfaces, implementing parallel programming techniques to handle multilayered surfaces, and reducing the computational cost of our HOPS/AWE algorithm. The analysis of multilayered periodic structures with numerous perturbation parameters will be an area of substantial interest for practitioners in the electromagnetic and engineering communities.
Download here
Published in SIAM Journal on Mathematical Analysis, 2023
The scattering of linear waves by periodic structures is a crucial phenomena in many branches of applied physics and engineering. In this paper we establish rigorous analytic results necessary for the proper numerical analysis of a class of High–Order Perturbation of Surfaces/Asymptotic Waveform Evaluation (HOPS/AWE) methods for #numerically simulating scattering returns from periodic diffraction gratings. More specifically, we prove a theorem on existence and uniqueness of solutions to a system of partial differential equations which model the interaction of linear waves with a periodic two–layer structure. Furthermore, we establish joint analyticity of these solutions with respect to both geometry and frequency perturbations. This result provides hypotheses under which a rigorous numerical analysis could be conducted on our recently developed HOPS/AWE algorithm.
Download here
Published in Journal of Scientific Computing, 2024
The scattering of electromagnetic radiation by a layered periodic diffraction grating is an important model in engineering and the sciences. The numerical simulation of this experiment has been widely explored in the literature and we advocate for a novel interfacial method which is perturbative in nature. More specifically, we extend a recently developed High–Order Perturbation of Surfaces/Asymptotic Waveform Evaluation (HOPS/AWE) algorithm to utilize a stabilized numerical scheme which also suggests a rigorous convergence result. An implementation of this algorithm is described, validated, and utilized in a sequence of challenging and physically relevant numerical experiments.
Download here
Published:
Described how to calculate the radiant of a meteor shower through astrometry and parallax (to determine the height of the meteors). CUREA Reflections 2013.
Published:
Review of this paper and various properties of the Riemann-Siegel formula.
Published:
Presented work done on supercomputers as a summer intern at ANL. Slides.
Published:
Summary of work done as a summer intern at CRREL. Slides.
Published:
Overview of the High-Order Pertubation of Surfaces (HOPS) schemes and their relation to Spectral Element Methods.
Published:
Properties of Pseudo-Differential Operators in $\mathbb R^n$.
Published:
Overview of Pseudo-Differential Operators in Euclidean Space.
Published:
An overview of the Shallow-Water Equations in relation to Tsunamis.
Published:
Summary of the Euler-Maclaurin Summation Formula, Riemann–Siegel Formula, and Odlyzko–Schonhage Algorithm in relation to calculating zeros of the Riemann zeta function. Slides.
Published:
General overview of wave scattering in periodic media. Slides.
Published:
Defended work on wave scattering in periodic media. Slides.
Published:
A fundamental problem when building a computer vision application is that of interpretability. This talk discussed various ways machine learning models can make results easier to interpret by humans. Slides.
Published:
This talk discussed time series forecasting, automatic learning of temporal dependence, and how neural networks are able to automatically learn arbitrary complex mappings from inputs to outputs and support multiple inputs and outputs.
Published:
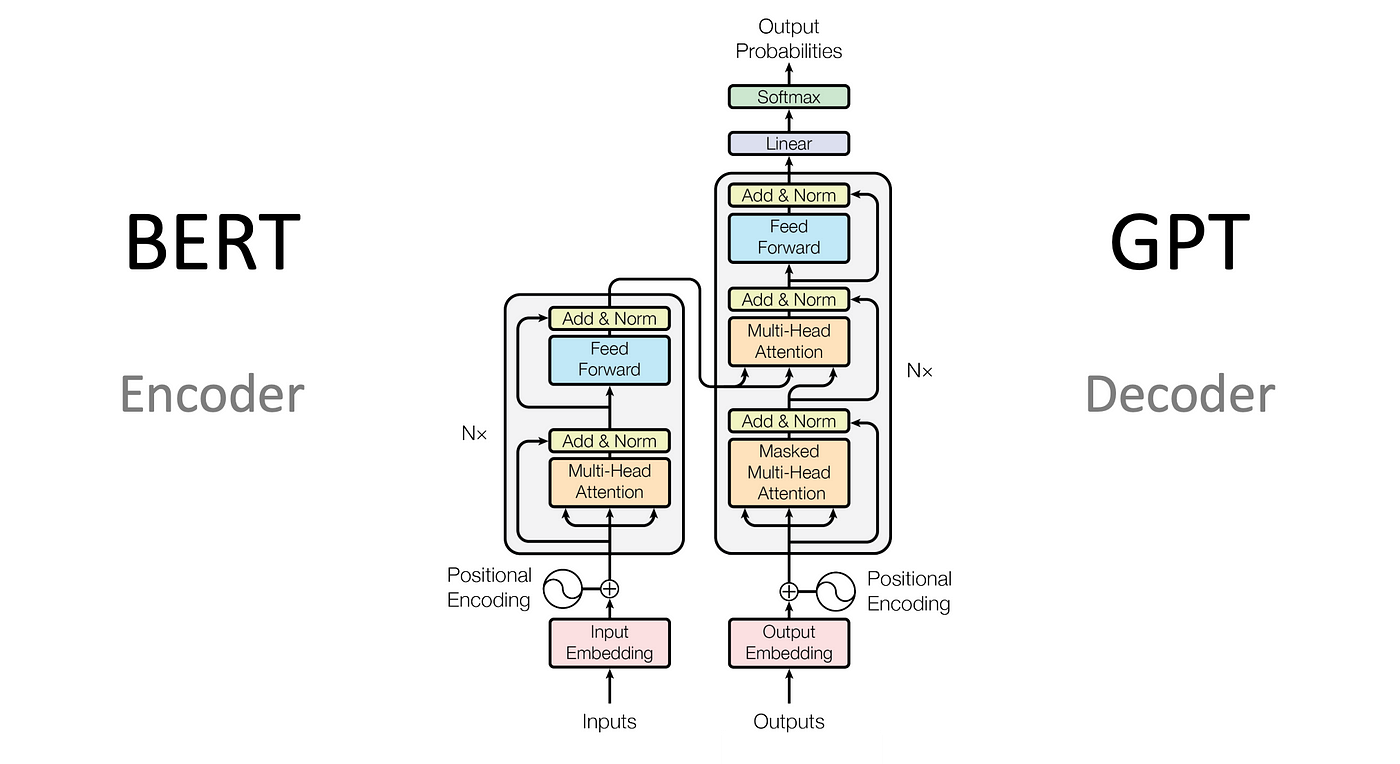
This talk described the encoder-decoder architecture for Transformers and self-attention as a weighted combination of all word embeddings. In addition, several advantages were presented over RNNs and ConvNets.
Published:
This presentation explored a supervised machine learning regression project forecasting global average temperatures using historical meteorological data spanning over a century. Without relying on existing weather forecasts, the project leverages historical global temperature averages (land, ocean, maximum, and minimum) to build and evaluate multiple regression models including Linear Regression, KNN, Random Forest, SVM, and Gradient Boosting, culminating in an analysis of the best performing model with partial dependence plots. Notebook.
Published:
This talk summarized neural style transfer and variational autoencoders for image generation, image augmentation, and image blending. In addition, we also reviewed a supervised learning project focused on predicting future land and ocean temperatures using multiple regression models with US temperature data.
Published:
This talk summarized different aspects and intricacies of generative adversarial networks and a unsupervised machine project for classifying mall customers by clustering.
Published:
Explored key methods to boost model performance, such as hyperparameter tuning and model ensembling. Additionally, we reviewed ways to speed up and scale training using multi-GPU and TPU setups, mixed precision, and cloud computing resources.
Published:
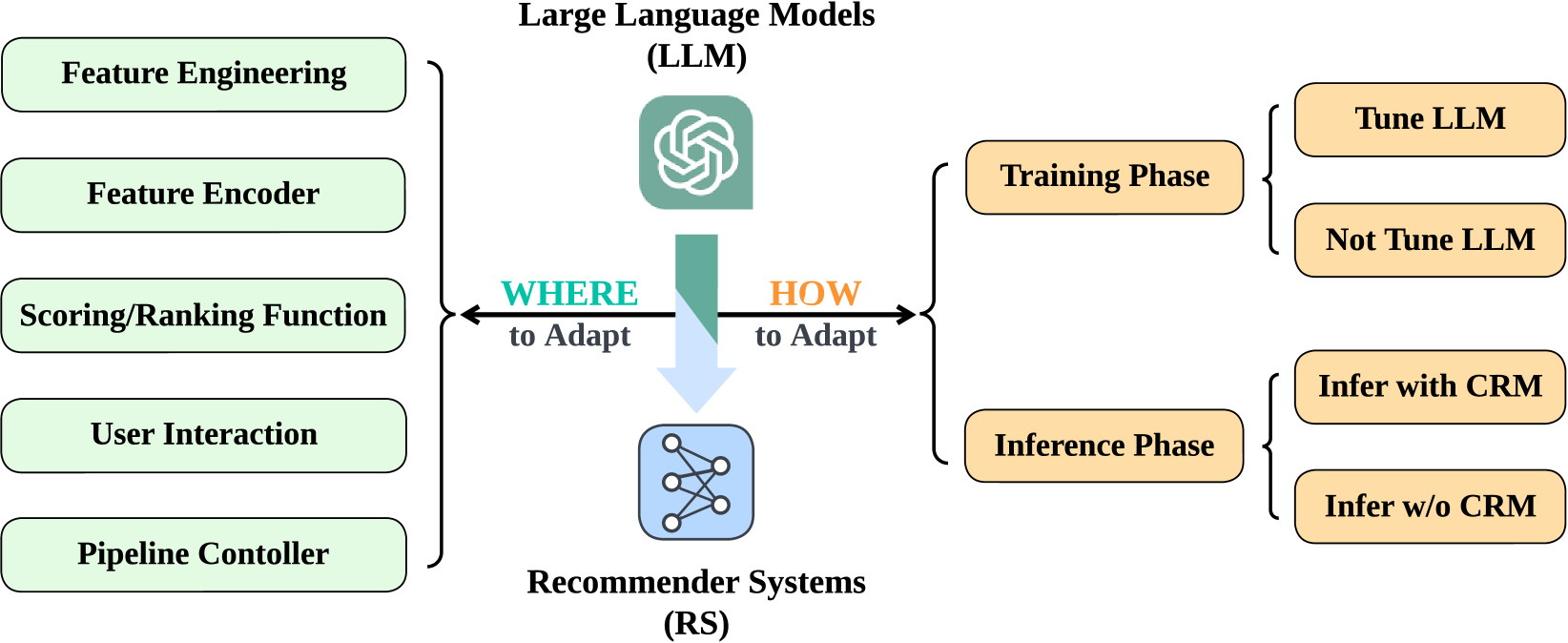
Built a NLP Information Retrieval System through user reviews through the popular Trip Advisor website. Notebook 1, Notebook 2, Dash App.
Published:
Explored the fundamentals of transformers and their application through pretrained models using Hugging Face. Reviewed key concepts and practical methodologies, providing a foundation for integrating these models into various machine learning workflows.
Published:
Covered the fundamental concepts of Transformer models, including tokenization and attention mechanisms. Learned how to use tokenizers to convert text into model-friendly tensors and explored the interaction between tokenizers and models for generating predictions. Reviewed important aspects such as input IDs and attention masks, building a foundation for navigating the Hugging Face documentation and implementing these models in machine learning tasks.
Published:
Discussed career opportunities for mathematical scientists in business, entrepreneurship, government, industry, and nonprofit settings with students and postdoctoral scholars, as well as how mathematics departments can enhance their curriculum and training to prepare their graduates for success in diverse professional environments. AMS Special Session.
Published:
Physics-Informed Neural Networks (PINNs) have transformed the numerical solution of partial differential equations (PDEs) by embedding them as soft constraints within the neural network training process. This approach has made PINNs a key component of the scientific machine learning (SciML) ecosystem. In this talk, we provide a broad overview of the PINN architecture, followed by three examples from physical systems: a damped oscillator with sinusoidal forcing, the Helmholtz equation, and a second-order elliptic eigenvalue problem known as the Gross-Pitaevskii equation. Furthermore, we demonstrate how PINNs can be used in practice and discuss key challenges, such as automatic weight selection via self-adaptive weight balancing, selecting the appropriate optimizer, and irregular boundary conditions. Notebook.
Published:
Single-head self-attention computes attention using a single set of query, key, and value projections, capturing global dependencies in one representation space. In contrast, multi-head self-attention uses multiple parallel attention heads, each with distinct projections, allowing the model to learn diverse patterns and relationships from different subspaces. This architectural enhancement significantly improves the model’s ability to capture complex contextual information, which is critical for tasks in natural language understanding.
Published:
This talk explored how to share and load models, tokenizers, and datasets using the Hugging Face Hub, enabling collaboration across the NLP community. It also highlighted the power of the datasets library in simplifying data access, preprocessing, and integration into end-to-end machine learning workflows.
Published:
This presentation covered the process of generating song lyrics by fine-tuning a custom GPT-2 model on lyrics from specific artists such as Blink-182 and Weird Al Yankovic. It covered data scraping, preprocessing, model training using the Hugging Face Transformers library, and generating structured lyrical content. The workflow concluded with training a custom GPT model specifically on Taylor Swift lyrics to produce original lyrics in her style. Notebook
Published:
This talk analyzed the Wisconsin Breast Cancer Diagnostic dataset to develop a supervised machine learning classification model that predicts whether breast masses are benign or malignant based on cellular characteristics extracted from digitized images. Several algorithms were tested including Logistic Regression, KNN, Random Forest, Support Vector Machine, and XGBoost, with Logistic Regression emerging as the best performer, improving accuracy from a baseline of 62.6% to 98.25%. The analysis demonstrates the effectiveness of machine learning for breast cancer diagnosis and suggests further research directions including applying similar techniques to other cancer types, comparing with other datasets, adding features like age and health, and analyzing feature-feature correlations. Notebook.
Published:
This talk covered the essential post-construction steps of preparing a Large Language Model for practical use, starting with pretraining. This involved training the model on unlabeled data for next-word prediction and introducing text generation techniques like temperature scaling and Top-k sampling. The talk then covered detailed classification fine-tuning, where the model’s architecture is modified by adding a classification head and freezing the main weights to specialize it for supervised tasks like spam detection. Together, these concepts illustrate the transformation of a base GPT model into both a creative text generator and a practical text classifier. Notebook
Published:
The talk summarized the process of Instruction Fine-Tuning, which is necessary to convert a pre-trained LLM from a general text completer into a model capable of following specific human commands. The core method involves preparing a supervised dataset of explicit instruction-input-response pairs and then fine-tuning a pre-trained model on this formatted data. The model’s weights are adjusted to reliably produce the desired response for a given instruction. The final step is evaluating the model’s ability to follow instructions using automated conversational scoring techniques, often by employing another LLM to grade the quality of the generated responses. Notebook
Published:
The talk introduced Perturbative Learning PINNs (PL-PINNs), which train a neural network to learn only the correction $\psi$ to a known base solution $v$, writing the total solution as $u=v+\psi$. The core method is a continuation-based training strategy that gradually shifts the problem from a simple, solvable regime to the complex, nonlinear target problem, thereby avoiding poor local minima. A hybrid scaling strategy was also detailed, allowing the method to transition from high, perturbation-level accuracy in simple cases to flexible, adaptive learning in highly nonlinear regimes. Overall, PL-PINNs solve challenging nonlinear problems, like the Gross–Pitaevskii equation, more efficiently and robustly than standard PINNs.
Published:
This talk introduced the concept of low-rank approximation for tensors and matrices, which utilizes algebraic decompositions like Singular Value Decomposition (SVD) to represent high-dimensional data using a minimal set of essential components. The core method is a geometric approach to dimensionality reduction that identifies eigenvectors and eigenvalues to isolate principal directions of variance within a linear transformation. A visualization-driven intuition for coordinate scaling and space reshaping was also presented, providing information about how high-rank data can be compressed into lower-dimensional subspaces without significant information loss. Overall, low-rank approximations solve challenges in data redundancy and computational complexity, such as in text vectorization (e.g., RETVec) or image processing, more efficiently and robustly than standard full-rank representations. Notebook.
Workshop, UIC, Department of Mathematics, Statistics, and Computer Science (MSCS), 2018
Led recitation sessions and assisted students with rules defining the natural logarithm and exponential function.
Workshop, UIC, Department of Mathematics, Statistics, and Computer Science (MSCS), 2019
Led recitation sessions and assisted students with techniques and applications of ordinary and partial differential equations.
Workshop, UIC, Department of Mathematics, Statistics, and Computer Science (MSCS), 2020
Led recitation sessions and assisted students with concepts in mathematical modeling and applications to biology.
Workshop, UIC, Department of Mathematics, Statistics, and Computer Science (MSCS), 2020
Led weekly Matlab sessions and discussed numerical algorithms.
Workshop, UIC, Department of Mathematics, Statistics, and Computer Science (MSCS), 2021
Led recitation sessions and assisted students with conceptual information in calculus. My student reviews are here.