Matthew Kehoe

Matthew Kehoe

Data and research scientist with a background in computational mathematics. Passionate about machine learning and scientific software development.

Sitemap

A list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.

Pages

Posts

portfolio

Computational Electromagnetics

Published:

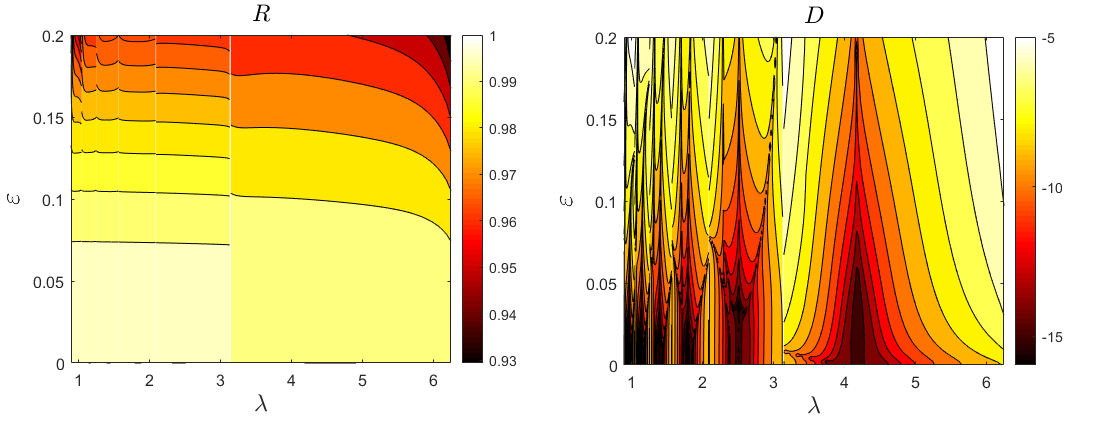
A High–Order Perturbation of Surfaces/Asymptotic Waveform Evaluation (HOPS/AWE) algorithm for Grating Scattering Problems.

Computational Number Theory

Published:

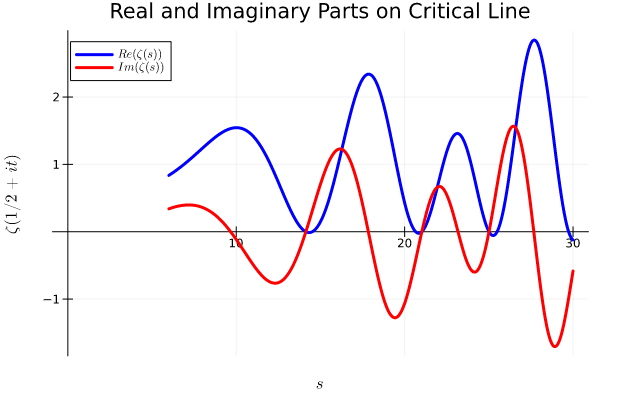
Computer implementation of the Riemann Siegel formula in Julia alongside various plotting and numerical programs related to the Riemann zeta function.

Data Science and Machine Learning

Published:

A collection of ML projects including linear/logistic regression, time series analysis, natural language processing, unsupervised ML, self-supervised ML, and LLMs.

NLP Recommender System

Published:

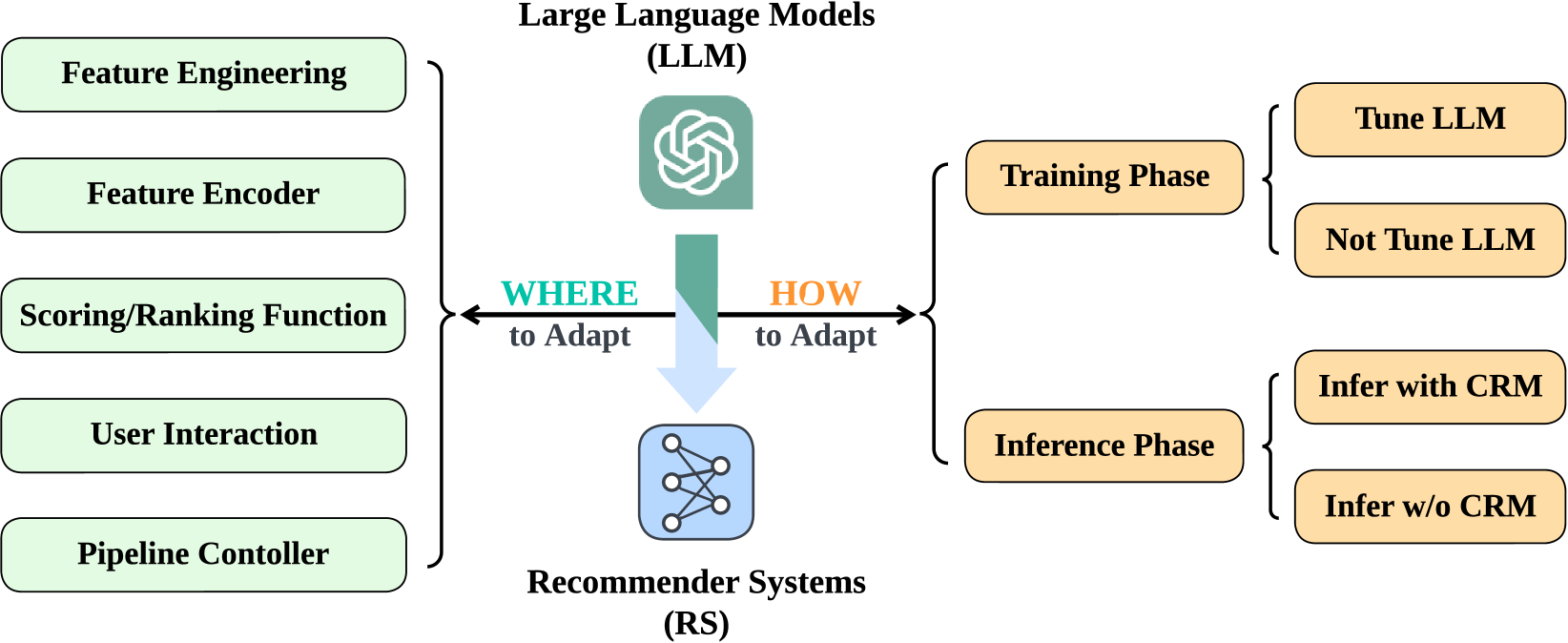
A recommender system for travel destinations through the popular website Trip Advisor.

publications

Computational Methods for the Riemann Zeta Function

Published in University of Michigan Deep Blue System, 2015

This project focuses on exploring different computational methods of the Riemann Zeta function. The zeta function is formally defined as $\zeta(s)$ and the Riemann Hypothesis states that all non-trivial zeros of $\zeta(s)$ lie on the critical line where $\Re(s) = 1/2$. Modern research and advanced algorithms have not been able to disprove the Riemann Hypothesis. More recently, a variation of the Odlyzko-–Schönhage algorithm has verified the Riemann Hypothesis up to $10^{13}$ zeros. This project is composed of two major programs which calculate functional values and zeros of the Riemann zeta function. The first program calculates $\zeta(s)$ for any value of $s$ provided $s\in\mathbb{R}$ through what is known as the Cauchy-Schlömilch transformation. The second program uses the well known Riemann–Siegel formula. Prior to the work done inside the Odlyzko–Schönhage algorithm, this was the method of choice for finding zeros of $\zeta(s)$. The algorithm is heavily dependent on locating sign changes of the Riemann-Siegel $Z$ function in order to find zeros on the critical line. Loosely speaking, one can derive this formula from a direct relationship that was originally found by Siegel which states that $Z(t) = e^{i \theta(t)} \zeta\left(\frac{1}{2}+it\right)$.

Download here

Joint Analyticity of the Transformed Field and Dirichlet–Neumann Operator in Periodic Media

Published in UIC Electronic Thesis and Dissertation (ETD) System, 2022

This thesis presents rigorous analytical and numerical results necessary for the numerical analysis of a class of High–Order Perturbation of Surfaces/Asymptotic Waveform Evaluation (HOPS/AWE) methods in a laterally periodic two–layer structure. Numerical simulations of scattering returns from periodic diffraction gratings are crucial to a large number of applications in physics and engineering, and the work presented here examines methods for numerically modeling scattering returns from such structures. The strategies presented in this thesis represent the results of our efforts towards the dual goals of 1) Proving a theorem on the existence and uniqueness of solutions to a system of partial differential equations which model the interaction of linear waves in periodic layered media and 2) Developing a numerical algorithm to record scattered energy through a novel interfacial method that is perturbative in nature. The first of our goals is established through classical methods based on the theory of Sobolev spaces and regular perturbation theory. The proof involves several rigorous analyses, and we formulate the scattering problem in terms of Dirichlet–Neumann Operators which are computed using the Transform Field Expansion methodology. A novelty of our approach is the joint analyticity of solutions with respect to both geometry and frequency perturbations. The theory itself is then validated through our second goal which is the development of a joint HOPS/AWE algorithm. For this, we develop a special class of interfacial numerical algorithms that are well–suited to periodic diffraction problems. Our algorithm calculates the Reflectivity Map, $R$, which measures the response (reflected energy) of a periodically corrugated grating structure as a function of its illumination frequency. Moreover, we present a series of challenging and physically relevant numerical experiments to validate the scattering results expected by our algorithm. Forthcoming research will focus on extending the proof of analyticity to additional parameters relevant to the geometry of the structure, increasing the complexity of the structure through generalizing our results to any finite number of layered interfaces, implementing parallel programming techniques to handle multilayered surfaces, and reducing the computational cost of our HOPS/AWE algorithm. The analysis of multilayered periodic structures with numerous perturbation parameters will be an area of substantial interest for practitioners in the electromagnetic and engineering communities.

Download here

Joint Geometry/Frequency Analyticity of Fields Scattered by Periodic Layered Media

Published in SIAM Journal on Mathematical Analysis, 2023

The scattering of linear waves by periodic structures is a crucial phenomena in many branches of applied physics and engineering. In this paper we establish rigorous analytic results necessary for the proper numerical analysis of a class of High–Order Perturbation of Surfaces/Asymptotic Waveform Evaluation (HOPS/AWE) methods for #numerically simulating scattering returns from periodic diffraction gratings. More specifically, we prove a theorem on existence and uniqueness of solutions to a system of partial differential equations which model the interaction of linear waves with a periodic two–layer structure. Furthermore, we establish joint analyticity of these solutions with respect to both geometry and frequency perturbations. This result provides hypotheses under which a rigorous numerical analysis could be conducted on our recently developed HOPS/AWE algorithm.

Download here

A Stable High-Order Perturbation of Surfaces/Asymptotic Waveform Evaluation Method for the Numerical Solution of Grating Scattering Problems

Published in Journal of Scientific Computing, 2024

The scattering of electromagnetic radiation by a layered periodic diffraction grating is an important model in engineering and the sciences. The numerical simulation of this experiment has been widely explored in the literature and we advocate for a novel interfacial method which is perturbative in nature. More specifically, we extend a recently developed High–Order Perturbation of Surfaces/Asymptotic Waveform Evaluation (HOPS/AWE) algorithm to utilize a stabilized numerical scheme which also suggests a rigorous convergence result. An implementation of this algorithm is described, validated, and utilized in a sequence of challenging and physically relevant numerical experiments.

Download here

talks

Interpreting what convnets learn

Published:

A fundamental problem when building a computer vision application is that of interpretability. This talk discussed various ways machine learning models can make results easier to interpret by humans. Slides.

Deep Learning for Timeseries

Published:

This talk discussed time series forecasting, automatic learning of temporal dependence, and how neural networks are able to automatically learn arbitrary complex mappings from inputs to outputs and support multiple inputs and outputs.

Transformers and Natural Language Processing

Published:

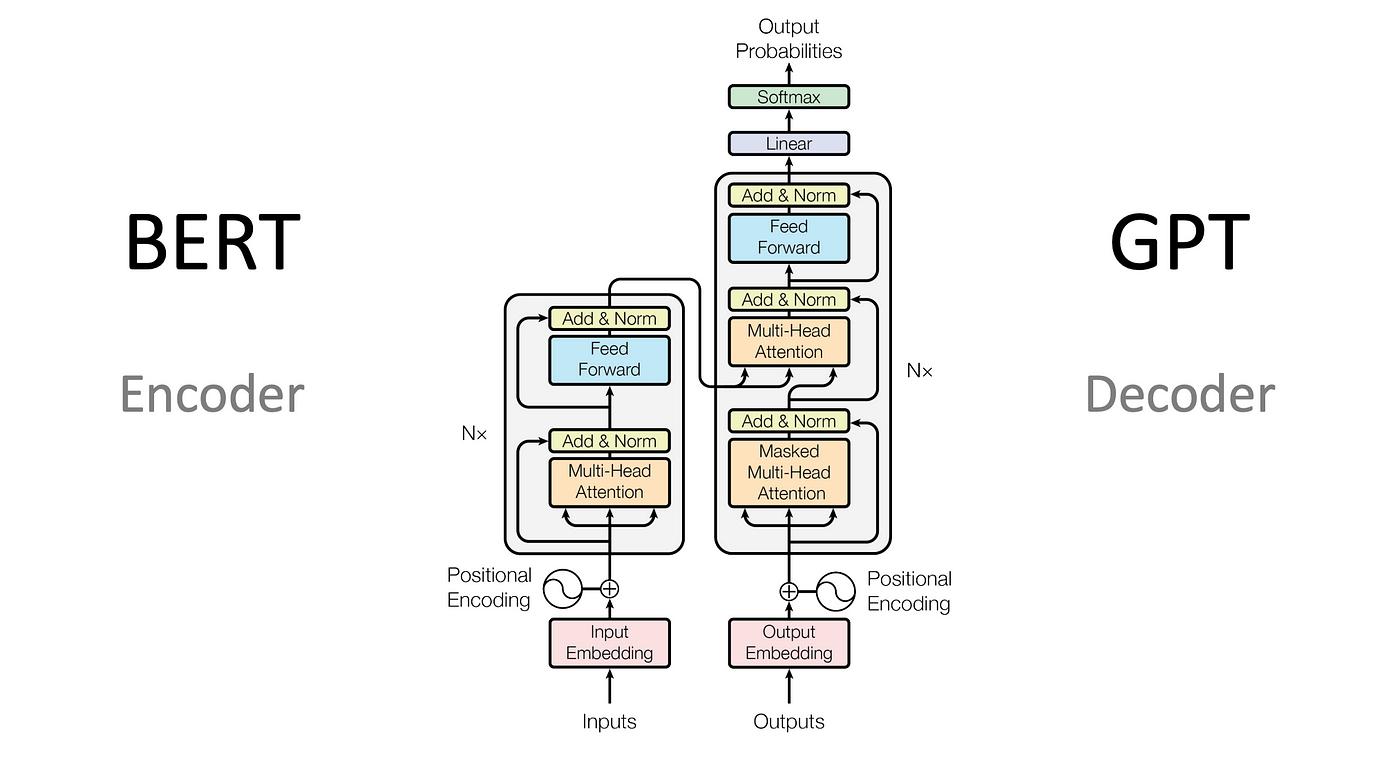
This talk described the encoder-decoder architecture for Transformers and self-attention as a weighted combination of all word embeddings. In addition, several advantages were presented over RNNs and ConvNets.

Neural Style Transfer, Variational Autoencoders, and Supervised Learning

Published:

This talk summarized neural style transfer and variational autoencoders for image generation, image augmentation, and image blending. In addition, we also reviewed a supervised learning project focused on predicting future land and ocean temperatures using multiple regression models with US temperature data.

Scaling-up model training with GPUs and TPUs

Published:

Explored key methods to boost model performance, such as hyperparameter tuning and model ensembling. Additionally, we reviewed ways to speed up and scale training using multi-GPU and TPU setups, mixed precision, and cloud computing resources.

Transformers and pretrained models with Hugging Face

Published:

Explored the fundamentals of transformers and their application through pretrained models using Hugging Face. Reviewed key concepts and practical methodologies, providing a foundation for integrating these models into various machine learning workflows.

Tokenization, Sequences, and Attention Masks with Hugging Face

Published:

Covered the fundamental concepts of Transformer models, including tokenization and attention mechanisms. Learned how to use tokenizers to convert text into model-friendly tensors and explored the interaction between tokenizers and models for generating predictions. Reviewed important aspects such as input IDs and attention masks, building a foundation for navigating the Hugging Face documentation and implementing these models in machine learning tasks.

teaching

Math 121: Precalculus (1 Semester)

Workshop, UIC, Department of Mathematics, Statistics, and Computer Science (MSCS), 2018

Led recitation sessions and assisted students with rules defining the natural logarithm and exponential function.

Math 220: Differential Equations (1 Semester)

Workshop, UIC, Department of Mathematics, Statistics, and Computer Science (MSCS), 2019

Led recitation sessions and assisted students with techniques and applications of ordinary and partial differential equations.

Math 419: Mathematical Biology (1 Semester)

Workshop, UIC, Department of Mathematics, Statistics, and Computer Science (MSCS), 2020

Led recitation sessions and assisted students with concepts in mathematical modeling and applications to biology.

Math 180: Calculus 1 (4 Semesters)

Workshop, UIC, Department of Mathematics, Statistics, and Computer Science (MSCS), 2021

Led recitation sessions and assisted students with conceptual information in calculus. My student reviews are here.